Інтеграли від тригонометричних функцій.
Приклади рішень

На даному уроці ми розглянемо інтеграли від тригонометричних функцій, тобто начинкою інтегралів у нас будуть синуси, косінуси, тангенси та котангенси у різних комбінаціях. Всі приклади будуть розібрані докладно, доступно та зрозуміло навіть для чайника.

Для успішного вивчення інтегралів від тригонометричних функцій Ви повинні добре орієнтуватися у найпростіших інтегралах, а також мати деякі прийоми інтегрування. Ознайомитись із цими матеріалами можна на лекціях Невизначений інтеграл. Приклади рішеньта .

А зараз нам знадобляться: Таблиця інтегралів, Таблиця похіднихі Довідник тригонометричних формул. Усі методичні посібники можна знайти на сторінці Математичні формули та таблиці. Рекомендую все надрукувати. Особливо загострюю увагу на тригонометричних формулах, вони мають бути перед очима– без цього ефективність роботи помітно зменшиться.

Але спочатку про те, яких інтегралів у цій статті ні. Тут не знайдеться інтегралів виду, - косинус, синус, помножений на якийсь багаточлен (рідше що-небудь з тангенсом або котангенсом). Такі інтеграли інтегруються частинами, і для вивчення методу відвідайте урок Інтегрування частинами. Приклади рішень .Також тут не знайдеться інтегралів з «арками» – арктангенсом, арксинусом та ін, вони теж найчастіше інтегруються частинами.

При знаходженні інтегралів від тригонометричних функцій використовують ряд методів:

(4) Використовуємо табличну формулу , єдина відмінність, замість «ікса» у нас складний вираз.

Приклад 2

Приклад 3

Знайти невизначений інтеграл.

Класика жанру для тих, хто тоне на заліку. Як Ви, мабуть, помітили, у таблиці інтегралів немає інтеграла від тангенсу та котангенсу, проте такі інтеграли знайти можна.

(1) Використовуємо тригонометричну формулу

(2) Підбиваємо функцію під знак диференціалу.

(3) Використовуємо табличний інтеграл .

Приклад 4

Знайти невизначений інтеграл.

Це приклад для самостійного рішення, повне рішення та відповідь – наприкінці уроку.

Приклад 5

Знайти невизначений інтеграл.

Ступені у нас потихеньку підвищуватимуться =).
Спочатку рішення:

(1) Використовуємо формулу

(2) Використовуємо основне тригонометричне тотожність , з якого випливає, що .

(3) Почленно ділимо чисельник на знаменник.

(4) Використовуємо якість лінійності невизначеного інтеграла.

(5) Інтегруємо за допомогою таблиці.

Приклад 6

Знайти невизначений інтеграл.

Це приклад для самостійного рішення, повне рішення та відповідь – наприкінці уроку.

Також існують інтеграли від тангенсів і котангенсів, які знаходяться у вищих ступенях. Інтеграл від тангенсу в кубі розглянуто на уроці Як обчислити площу плоскої фігури?Інтеграли від тангенсу (котангенсу) у четвертому та п'ятому ступенях можна роздобути на сторінці Складні інтеграли.

Зниження ступеня підінтегральної функції

Даний прийом працює, коли підінтегральні функції нафаршировані синусами та косинусами в парнихступенях. Для зниження ступеня використовують тригонометричні формули , і , причому остання формула частіше використовується у зворотному напрямку: .

Приклад 7

Знайти невизначений інтеграл.

Рішення:

В принципі нічого нового тут немає, за винятком того, що ми застосували формулу (зменшивши ступінь підінтегральної функції). Зверніть увагу, що я скоротив рішення. У міру накопичення досвіду інтеграл можна знаходити усно, це економить час і цілком припустимо при чистовому оформленні завдань. В даному випадку доцільно не розписувати і правило спочатку усно беремо інтеграл від 1, потім - від .

Приклад 8

Знайти невизначений інтеграл.

Це приклад для самостійного рішення, повне рішення та відповідь – наприкінці уроку.

Такі обіцяне підвищення ступеня:

Приклад 9

Знайти невизначений інтеграл.

Спочатку рішення, потім коментарі:

(1) Готуємо підінтегральну функцію для застосування формули .

(2) Власне застосовуємо формулу.

(3) Зводимо знаменник квадрат і виносимо константу за знак інтеграла. Можна було зробити трохи інакше, але, як на мене, так зручніше.

(4) Використовуємо формулу

(5) У третьому доданку знову знижуємо ступінь, але вже за допомогою формули .

(6) Наводимо подібні доданки (тут я почленно розділив та виконав додавання ).

(7) Власне беремо інтеграл, правило лінійності та метод підведення функції під знак диференціала виконуємо усно.

(8) Зачісуємо відповідь.

! У невизначеному інтегралі нерідко можна записати відповідь декількома способами

У прикладі остаточну відповідь можна було записати інакше – розкрити дужки і навіть це зробити ще до інтегрування виразу, тобто цілком допустима наступна кінцівка прикладу:

Цілком можливо, що такий варіант навіть зручніший, просто я пояснив так, як сам звик вирішувати). Ось ще один характерний приклад для самостійного вирішення:

Приклад 10

Знайти невизначений інтеграл.

Це приклад вирішується двома способами, і у Вас можуть вийти дві абсолютно різні відповіді(точніше кажучи, вони виглядатимуть абсолютно по-різному, а з математичної точки зору є еквівалентними). Швидше за все, Ви не побачите найбільш раціональний спосіб і помучитеся із розкриттям дужок, використанням інших тригонометричних формул. Найбільш ефективне рішення наведено наприкінці уроку.

Підсумовуючи параграф, зробимо висновок: будь-який інтеграл виду , де і - парнічисла, вирішується шляхом зниження ступеня підінтегральної функції.
Насправді мені зустрічалися інтеграли з 8 і 10 ступенями, вирішувати їх страшний гемор доводилося, знижуючи рівень кілька разів, у результаті виходили довгі-довгі відповіді.

Метод заміни змінної

Як уже згадувалося у статті Метод заміни змінної у невизначеному інтегралі, Основною причиною використання методу заміни є те що, що у подинтегральном вираженні є певна функція та її похідна :
(функції, не обов'язково перебувають у творі)

Приклад 11

Знайти невизначений інтеграл.

Дивимося в таблицю похідних і помічаємо формули, , тобто, у нашому підінтегральному вираженні є функція та її похідна. Однак ми бачимо, що при диференціюванні косинус та синус взаємно перетворюються один на одного, і виникає питання: як виконати заміну змінної і що ж позначати за – синус чи косинус?! Питання можна вирішити методом наукового тику: якщо ми неправильно виконаємо заміну, то нічого хорошого не вдасться.

Загальний орієнтир: у схожих випадках потрібно позначити функцію, яка знаходиться в знаменнику.

Перериваємо рішення та проводимо заміну

У знаменнику у нас все добре, все залежить тільки від , тепер залишилося з'ясувати, на що перетвориться.
Для цього знаходимо диференціал:

Або якщо коротше:
З отриманої рівності за правилом пропорції висловлюємо потрібне нам вираз:

Отже:

Тепер все підінтегральне вираження у нас залежить тільки від і можна продовжувати рішення

Готово. Нагадую, що мета заміни – спростити підінтегральне вираження, у разі все звелося до інтегрування статечної функції по таблиці.

Я не випадково так докладно розписав цей приклад, це зроблено з метою повторення та закріплення матеріалів уроку Метод заміни змінної у невизначеному інтегралі.

А зараз два приклади для самостійного вирішення:

Приклад 12

Знайти невизначений інтеграл.

Приклад 13

Знайти невизначений інтеграл.

Повні рішення та відповіді наприкінці уроку.

Приклад 14

Знайти невизначений інтеграл.

Тут знову в підінтегральному вираженні знаходяться синус з косинусом (функція з похідною), але вже у творі, і виникає дилема – що позначати за , синус чи косинус?

Можна спробувати провести заміну методом наукового тику, і якщо нічого не вийде, то позначити за іншу функцію, але є:

Загальний орієнтир: потрібно позначити ту функцію, яка, образно кажучи, знаходиться в «незручному положенні».

Ми бачимо, що в даному прикладі студент косинус «мучиться» від ступеня, а синус – так сидить, сам по собі.

Тому проведемо заміну:

Якщо у кого залишилися труднощі з алгоритмом заміни змінної та знаходженням диференціалу, слід повернутися до уроку Метод заміни змінної у невизначеному інтегралі.

Приклад 15

Знайти невизначений інтеграл.

Аналізуємо підінтегральну функцію, що необхідно позначити за ?
Згадуємо наші орієнтири:
1) Функція, швидше за все, знаходиться у знаменнику;
2) Функція перебуває у «незручному положенні».

До речі, ці орієнтири справедливі як для тригонометричних функцій.

Під обидва критерії (особливо під другий) підходить синус, тому напрошується заміна. В принципі, заміну можна вже проводити, але спочатку непогано було б розібратися, а що робити з ? По-перше, «відщипуємо» один косинус:

Ми резервуємо під наш «майбутній» диференціал

А виражаємо через синус за допомогою основного тригонометричного тотожності:

Ось тепер заміна:

Загальне правило: Якщо в підінтегральній функції одна з тригонометричних функцій (синус або косинус) знаходиться в непарноюступеня, то потрібно від непарного ступеня «відкусити» одну функцію, а потім – позначити іншу функцію.Йдеться лише про інтеграли, де є косинуси та синуси.

У розглянутому прикладі непарною мірою у нас знаходився косинус, тому ми відщипнули від ступеня один косинус, а за позначили синус.

Приклад 16

Знайти невизначений інтеграл.

Ступені йдуть на зліт =).
Це приклад самостійного рішення. Повне рішення та відповідь наприкінці уроку.

Універсальна тригонометрична підстановка

Універсальна тригонометрична підстановка – це найчастіший випадок методу заміни змінної. Її можна спробувати застосувати, коли не знаєш, що робити. Але насправді є деякі орієнтири для її застосування. Типовими інтегралами, де потрібно застосувати універсальну тригонометричну підстановку, є такі інтеграли: , , , і т.д.

Приклад 17

Знайти невизначений інтеграл.

Універсальна тригонометрична підстановка у разі реалізується в такий спосіб. Проведемо заміну: . Я використовую не букву, а букву, це не є якимось правилом, просто знову ж таки я так звик вирішувати.

Тут зручніше знаходити диференціал, для цього з рівності, я висловлюю:
Навішую на обидві частини арктангенс:

Арктангенс та тангенс взаємно знищуються:

Таким чином:

На практиці можна не розписувати так детально, а просто користуватися готовим результатом:

! Вираз справедливий лише в тому випадку, якщо під синусами та косинусами у нас просто «ікси», для інтеграла (про яке ми ще поговоримо) все буде трохи інакше!

При заміні синуси та косинуси у нас перетворюються на такі дроби:
, , ці рівності засновані на відомих тригонометричних формулах: ,

Отже, чистове оформлення може бути таким:

Проведемо універсальну тригонометричну підстановку:

Будуть і завдання для самостійного вирішення, до яких можна переглянути відповіді.

Підінтегральний вираз можна перетворити з твору тригонометричних функцій на суму

Розглянемо інтеграли, в яких підінтегральна функція є твір синусів і косінусів першого ступеня від іксу, помноженого на різні множники, тобто інтеграли виду

Скориставшись відомими тригонометричними формулами

(2)
(3)
(4)
можна перетворити кожен із творів в інтегралах виду (31) в алгебраїчну суму та проінтегрувати за формулами

(5)

(6)

приклад 1.Знайти

Рішення. За формулою (2) при

приклад 2.Знайти інтеграл від тригонометричної функції

Рішення. За формулою (3) при

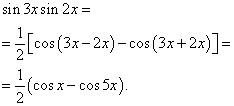
Приклад 3.Знайти інтеграл від тригонометричної функції

Рішення. За формулою (4) при отримуємо наступне перетворення підінтегрального виразу:

Застосовуючи формулу (6), отримаємо

Інтеграл твору ступенів синуса та косинуса одного і того ж аргументу

Розглянемо тепер інтеграли від функцій, що становлять твір ступенів синуса і косинуса однієї й тієї ж аргументу, тобто.

(7)

В окремих випадках один з показників ( mабо n) може дорівнювати нулю.

При інтегруванні таких функцій використовують те, що парний ступінь косинуса можна виразити через синус, а диференціал синуса дорівнює cos. x dx(або парний ступінь синуса можна виразити через косинус, а диференціал косинуса дорівнює - sin x dx ) .

Слід розрізняти два випадки: 1) хоча б один із показників mі nнепарний; 2) обидва показники парні.

Нехай має місце перший випадок, а саме показник n = 2k+ 1 – непарний. Тоді, враховуючи, що

Подинтегральное вираз представлено у вигляді, що його частина – функція лише синуса, іншу – диференціал синуса. Тепер за допомогою заміни змінної t= sin xрішення зводиться до інтегрування багаточлена щодо t. Якщо ж лише ступінь mнепарна, то чинять аналогічно, виділяючи множник sin x, висловлюючи решту підінтегральної функції через cos xі вважаючи t= cos x. Цей прийом можна використовувати і при інтегруванні приватного ступенів синуса та косинуса , коли хоча б один із показників - непарний . Вся річ у тому, що приватне ступенів синуса та косинуса - це окремий випадок їх твору : коли тригонометрична функція перебуває у знаменнику підинтегрального висловлювання, її ступінь - негативна. Але бувають і випадки приватного тригонометричних функцій, коли їх ступеня – лише парні. Про них – наступний абзац.

Якщо ж обидва показники mі n– парні, то, використовуючи тригонометричні формули

знижують показники ступеня синуса та косинуса, після чого вийде інтеграл того самого типу, що й вище. Тому інтегрування слід продовжувати за тією самою схемою. Якщо ж один із парних показників - негативний, тобто розглядається приватне парних ступенів синуса та косинуса, то дана схема не годиться . Тоді використовується заміна змінної в залежності від того, як можна перетворити підінтегральний вираз. Такий випадок буде розглянуто у наступному параграфі.

Приклад 4.Знайти інтеграл від тригонометричної функції

Рішення. Показник ступеня косинуса – непарний. Тому представимо

t= sin x(тоді dt= cos x dx ). Тоді отримаємо

Повертаючись до старої змінної, остаточно знайдемо

Приклад 5.Знайти інтеграл від тригонометричної функції

.

Рішення. Показник ступеня косинуса, як і попередньому прикладі – непарний, але більше. Уявимо

і зробимо заміну змінної t= sin x(тоді dt= cos x dx ). Тоді отримаємо

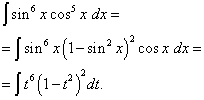
Розкриємо дужки

і отримаємо

Повертаючись до старої змінної, отримуємо рішення

Приклад 6.Знайти інтеграл від тригонометричної функції

Рішення. Показники ступеня синуса та косинуса – парні. Тому перетворимо підінтегральну функцію так:

Тоді отримаємо

У другому інтегралі зробимо заміну змінної, вважаючи t= sin2 x. Тоді (1/2)dt= cos2 x dx . Отже,

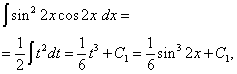
Остаточно отримуємо

Використання методу заміни зміною

Метод заміни змінноїпри інтегуванні тригонометричних функцій можна застосовувати у випадках, коли в підінтегральному вираженні присутній тільки синус або тільки косинус, твір синуса і косинуса, в якому або синус або косинус - в першому ступені, тангенс або котангенс, а також приватне парних ступенів синуса та косинуса одного і того ж аргументу. При цьому можна проводити перестановки не тільки x = tі sin x = t, але і tg x = tта ctg x = t .

Приклад 8.Знайти інтеграл від тригонометричної функції

.

Рішення. Зробимо заміну змінної: , Тоді . Підинтегральний вираз, що вийшов, легко інтегрується за таблицею інтегралів:

.

Приклад 9.Знайти інтеграл від тригонометричної функції

Рішення. Перетворимо тангенс у відношенні синуса та косинуса:

Зробимо заміну змінної: , Тоді . Підинтегральний вираз, що вийшов, являє собою табличний інтегралзі знаком мінус:

.

Повертаючись до початкової змінної, остаточно отримуємо:

.

Приклад 10Знайти інтеграл від тригонометричної функції

Рішення. Зробимо заміну змінної: , Тоді .

Перетворимо підінтегральний вираз, щоб застосувати тригонометричну тотожність :

Виробляємо заміну змінної, не забуваючи перед інтегралом поставити знак мінус (дивіться вище, чому одно dt). Далі розкладаємо підінтегральний вираз на множники та інтегруємо за таблицею:

Повертаючись до початкової змінної, остаточно отримуємо:

.

Знайти інтеграл від тригонометричної функції самостійно, а потім переглянути рішення

Універсальна тригонометрична підстановка

Універсальну тригонометричну підстановку можна застосовувати у випадках, коли підінтегральний вираз не підпадає під випадки, розібрані у попередніх параграфах. В основному, коли синус або косинус (або те й інше) знаходяться в знаменнику дробу. Доведено, що синус та косинус можна замінити іншим виразом, що містить тангенс половини вихідного кута наступним чином:

Але зауважимо, що універсальна тригонометрична підстановка часто тягне за собою досить складні перетворення алгебри, тому її краще застосовувати, коли ніякий інший метод не працює. Розберемо приклади, коли разом із універсальною тригонометричною підстановкою використовуються підведення під знак диференціалу та метод невизначених коефіцієнтів.

Приклад 12Знайти інтеграл від тригонометричної функції

.

Рішення. Рішення. Скористаємося універсальною тригонометричною підстановкою. Тоді
.

Дроби в чисельнику та знаменнику множимо на , а двійку виносимо і ставимо перед знаком інтеграла. Тоді

Докладно розглянуті приклади рішень інтегралів частинами, подинтегральное вираз яких є твором многочлена на експоненту (е ступеня х) чи синус (sin x) чи косинус (cos x).

Зміст

Див. також: Метод інтегрування частинами
Таблиця невизначених інтегралів
Методи обчислення невизначених інтегралів
Основні елементарні функції та їх властивості

Формула інтегрування частинами

При вирішенні прикладів цього розділу використовується формула інтегрування частинами:
;
.

Приклади інтегралів, що містять добуток багаточлена та sin x, cos x або e x

Ось приклади таких інтегралів:
, , .

Для інтегрування подібних інтегралів, многочлен позначають через u , а частину, що залишилася - через v dx . Далі застосовують формулу інтегрування частинами.

Нижче надається докладне рішення цих прикладів.

Приклади вирішення інтегралів

Приклад з експонентою, е в ступені х

Визначити інтеграл:
.

Введемо експоненту під знак диференціалу:
e - x dx = - e - x d(-x) = - d(e - x).

Інтегруємо частинами.

тут
.
Інтеграл, що залишився, також інтегруємо частинами.
.
.
.
Остаточно маємо:
.

Приклад визначення інтеграла із синусом

Обчислити інтеграл:
.

Введемо синус під знак диференціалу:

Інтегруємо частинами.

тут u = x 2 , v = cos(2 x+3), du = ( x 2 )′ dx

Інтеграл, що залишився, також інтегруємо частинами. І тому вводимо косинус під знак диференціала.


тут u = x, v = sin(2 x+3), du = dx

Остаточно маємо:

Приклад твору багаточлена та косинуса

Обчислити інтеграл:
.

Введемо косинус під знак диференціалу:

Інтегруємо частинами.

тут u = x 2 + 3 x + 5, v = sin 2 x, du = ( x 2 + 3 x + 5 )′ dx

Таблиця первісних ("інтегралів"). Таблиця інтегралів. Табличні невизначені інтеграли. (Найпростіші інтеграли та інтеграли з параметром). Формули інтегрування частинами. Формула Ньютона-Лейбніца.

Таблиця первісних ("інтегралів"). Табличні невизначені інтеграли. (Найпростіші інтеграли та інтеграли з параметром).
Інтеграл статечної функції.	Інтеграл статечної функції.
Інтеграл, що зводиться до інтегралу статечної функції, якщо загнати їх під знак диференціала.
	Інтеграли експоненти, де a-постійне число.
Інтеграл складної експонентної функції.	Інтеграл експонентної функції.
Інтеграл, що дорівнює натуральному логорифму.	Інтеграл: "Довгий логарифм".
	Інтеграл: "Довгий логарифм".
Інтеграл: "Високий логарифм".	Інтеграл, де х у чисельнику заводиться під символ диференціала (константу під знаком можна як додавати, так і віднімати), в результаті схожий з інтегралом, рівним натуральному логорифму.
Інтеграл: "Високий логарифм".
Інтеграл косинуса.	Інтеграл синусу.
Інтеграл, що дорівнює тангенсу.	Інтеграл, рівний котангенсу.
Інтеграл, рівний як арксинусу, так і арккосинусу
Інтеграл, рівний як арксинусу, і арккосинусу.	Інтеграл, рівний як арктангенсу, і арккотангенсу.
Інтеграл дорівнює косекансу.	Інтеграл, що дорівнює секансу.
Інтеграл, рівний арксеканс.	Інтеграл, рівний аркосекансу.
Інтеграл, рівний арксеканс.	Інтеграл, рівний арксеканс.
Інтеграл, що дорівнює гіперболічному синусу.	Інтеграл, що дорівнює гіперболічному косинусу.
Інтеграл, рівний гіперболічному синусу, де sinhx – гіперболічний синус в ангійській версії.	Інтеграл, рівний гіперболічному косинусу, де sinhx – гіперболічний синус в англійській версії.
Інтеграл, що дорівнює гіперболічному тангенсу.	Інтеграл, що дорівнює гіперболічному котангенсу.
Інтеграл, що дорівнює гіперболічному секансу.	Інтеграл, що дорівнює гіперболічному косекансу.

Формули інтегрування частинами. Правила інтегрування.

Формули інтегрування частинами. Формула Ньютона-Лейбніца. Правила інтегрування.
Інтегрування твору (функції) на постійну:
Інтегрування суми функцій:
невизначені інтеграли:
Формула інтегрування частинами певні інтеграли:
Формула Ньютона-Лейбніца певні інтеграли:	Де F(a),F(b)-значення первісних у точках b та a відповідно.

Таблиця похідних. Табличні похідні. Похідна робота. Похідна приватна. Похідна складна функція.

Якщо x – незалежна змінна, то:

Таблиця похідних. Табличні похідні. "Таблиця похідний" - так, на жаль, саме так їх і шукають в інтернеті
	Похідна статечної функції
	Похідна експоненти
Похідна складної експоненційної функції	Похідна експоненційна функція
Похідна логарифмічна функція	Похідна натуральна логарифма
	Похідна натурального логарифму функції
Похідна синуса	Похідна косинуса
Похідна косеканса	Похідна секанса
Похідна арксинуса	Похідна арккосинусу
Похідна арксинуса	Похідна арккосинусу
Похідна тангенса	Похідна котангенса
Похідна арктангенса	Похідна арккотангенса
Похідна арктангенса	Похідна арккотангенса
Похідна арксеканса	Похідна аркосеканса
Похідна арксеканса	Похідна аркосеканса
Похідна гіперболічного синуса Похідна гіперболічного синуса в англійській версії	Похідна гіперболічного косинуса Похідна гіперболічного косинуса в англійській версії
Похідна гіперболічного тангенсу	Похідна гіперболічного котангенсу
Похідна гіперболічного секансу	Похідна гіперболічного косекансу

Правила диференціювання. Похідна робота. Похідна приватна. Похідна складна функція.
Похідна робота (функції) на постійну:
Похідна суми (функцій):
Похідна робота (функцій):
Похідна приватного (функцій):
Похідна складної функції:

Властивості логарифмів. Основні формули логарифмів. Десяткові (lg) та натуральні логарифми (ln).

Основне логарифмічне тотожність
Покажемо як можна будь-яку функцію виду a b зробити експоненційною. Оскільки функція виду їх називається експоненційною, то
Будь-яка функція виду a b може бути представлена ​​у вигляді ступеня десяти

Натуральний логарифм ln (логарифм на основі е = 2,718281828459045…) ln(e)=1; ln(1)=0

Ряд Тейлора. Розкладання функції у ряд Тейлора.

Виявляється, більшість практично зустрічаютьсяматематичних функцій можуть бути з будь-якою точністю представлені на околицях деякої точки у вигляді статечних рядів, що містять ступеня змінної в порядку зростання. Наприклад, на околиці точки х=1:

При використанні рядів, званих рядами Тейлора,змішані функції, що містять, скажімо, алгебраїчні, тригонометричні та експоненційні функції, можуть бути виражені у вигляді суто алгебраїчних функцій. За допомогою рядів часто можна швидко здійснити диференціювання та інтегрування.

Ряд Тейлора на околиці точки a має види:

1) , Де f (x) - функція, що має при х = а похідні всіх порядків. R n - залишковий член у ряді Тейлора визначається виразом

2)

k-тий коефіцієнт (при х k) ряду визначається формулою

3) Приватним випадком низки Тейлора є ряд Маклорена (=Макларена) (Розкладання відбувається навколо точки а = 0)

при a=0

члени ряду визначаються за формулою

Умови застосування рядів Тейлора.

1. Для того, щоб функція f(x) могла бути розкладена в ряд Тейлора на інтервалі (-R;R) необхідно і достатньо, щоб залишковий член у формулі Тейлора (Маклорена) для цієї функції прагнув до нуля при k →∞ на вказаному інтервалі (-R;R).

2. Необхідно щоб існували похідні для цієї функції в точці, на околиці якої ми збираємося будувати ряд Тейлора.

Властивості рядів Тейлора.

Якщо f є аналітична функція, то її ряд Тейлора в будь-якій точці області визначення f сходить до f в деякій околиці а.

Існують нескінченно диференційовані функції, ряд Тейлора яких сходиться, але при цьому відрізняється від функції у будь-якій околиці а. Наприклад:

Ряди Тейлора застосовуються при апроксимації (наближення - науковий метод, що полягає у заміні одних об'єктів іншими, у тому чи іншому сенсі близькими до вихідних, але більш простими) функції багаточленів. Зокрема, лінеаризація ((від linearis - лінійний), один з методів наближеного уявлення замкнутих нелінійних систем, при якому дослідження нелінійної системи замінюється аналізом лінійної системи, у певному сенсі еквівалентної вихідної.) рівнянь відбувається шляхом розкладання в ряд Тейлора та відсікання всіх членів вище першого порядку.

Таким чином, практично будь-яку функцію можна представити у вигляді полінома із заданою точністю.

Приклади деяких поширених розкладів статечних функцій у ряди Маклорена (=Макларена, Тейлора на околицях точки 0) і Тейлора на околицях точки 1. Перші члени розкладів основних функцій у ряди Тейлора та Макларена.

Приклади деяких поширених розкладів статечних функцій у ряди Маклорена(=Макларена, Тейлора на околицях точки 0)

Приклади деяких поширених розкладів у ряди Тейлора на околицях точки 1