Вступ

З курсу планіметрії ми знаємо, що площина - це безліч, елементами якого є точки і в якому виконується система аксіом планіметрії, що описує властивості точок та прямі.

Простір - це безліч, елементами якого є точки і в якому виконується система аксіом стереометрії, що описує властивості точок, прямих та площин. Система аксіом стереометрії дає опис властивостей простору та його основних елементів. Поняття «точка», «пряма» та «площина» приймаються без визначень: їх опис та властивості містяться в аксіомах. З іншого боку, поняття «точка», «пряма», «площина» мають наочний сенс, відображений на кресленнях та малюнках.

Вивчення простору призводить до необхідності розширити систему аксіом планіметрії та розглянути нову групу аксіом, у яких виражені властивості взаємного розташування точок, прямих та площин, що особливо важливо для нас, у просторі.

Мета реферату - отримати наочне уявлення про простір та способи розташування площин у просторі.

Для виконання цієї мети поставлені такі завдання:

• - розглянути способи завдання площин у просторі,
• - Розглянути основні аксіоми стереометрії;
• - Вивчити можливі варіантивзаємного розташування площин у просторі,
• - сформулювати основні ознаки та властивості взаємного розташування площин у просторі;

Способи завдання площини

Вивчення простору призводить до потреби розширити систему аксіом.

Розглянемо аксіому R1. У просторі є площини. У кожній площині простору виконуються всі аксіоми планіметрії. Ця аксіома дає нам право розглядати у будь-якій площині простору відрізки, прямі з усіма їхніми властивостями, що вивчалися у планіметрії. Наприклад, якщо пряма а і точка М, що не належить їй, лежать у деякій площині б, то в цій площині можна провести через точку М пряму, паралельну до прямої а, і при цьому тільки одну.

В аксіомі R3 говориться: якою б не була площина, існують точки, що належать цій площині, і точки, що не належать їй. Даною аксіомою стверджується, що для будь-якої площини в просторі можна вибрати будь-яку кількість точок у цій площині, так само як і скільки завгодно точок поза нею. У разі, якщо точка А л7+їжить у (належить) площині б, то записують: А б і кажуть, що площина б проходить через точку А. Якщо точка А не належить площині б, то записують: А б і кажуть, що площина б не проходить через точку А.

Площина у просторі однозначно визначається:

Трьома точками, що не лежать на прямій. Аксіома R2 (аксіома площини) свідчить: Через будь-які три точки, що не належать до однієї прямої, можна провести площину, і до того ж лише одну. Площина, яка проходить через точки А, В і С, що не належать до однієї прямої (С АВ), позначається символічно (АВС); якщо цією площиною є площина б, пишуть б = (АВС) або (АВС) = б. Стіл, що має три ніжки, не може хитатися на плоскій підлозі. Його стійкість пояснюється тим, що кінці трьох ніжок (три точки) належать одній площині - площині підлоги, але не належать одній прямій. Погано зроблений стіл на чотирьох ніжках гойдається на плоскій підлозі, і під одну з його ніжок щось намагаються підкласти.

Прямий і крапкою, що не лежить на прямій.

По теоремі 1 через будь-яку пряму і точку, що не належить їй, можна провести площину, і притому тільки одну.

Теорема 2. Через будь-які дві прямі, що перетинаються, можна провести площину, і притому тільки одну.

Якщо пряма проходить через дві точки площини, вона лежить у цій площині

Теорема 3. Через дві паралельні прямі можна провести єдину площину.

Способи завдання площини, що однозначно визначають положення площини в просторі (див. рис. 16):

а) три точки, що не лежать на одній прямій;

б) пряма та точка поза прямою;

с) паралельні прямі;

d) прямі, що перетинаються.

е) пласка фігура;

На епюрі площина визначається проекціями перерахованих геометричних елементів і слідами. Ці елементи звуться визначника площини (∆).

Площина у просторі може бути задана слідами (див. мал. 17). За площиною називають лінію перетину даної площини з площиною проекцій. У системі трьох площин проекцій площина загального стану p(не перпендикулярна і не паралельна площин проекцій) може мати три сліди - горизонтальний ( р 1 ), фронтальний ( р 2 ), профільний ( р 3 ); Рх, Ру, Рz- Точки сходу слідів (рис. 17)

3.2. Площини приватного стану.

До площин приватного становища належать:

Проецірующие площини, тобто. площини, перпендикулярні до однієї із площин проекцій (рис. 18);

Площини рівня – площини, паралельні одній із площин проекцій (рис. 19).

3.3. Проєціруючі площини

Особливості проектуючих площин:

1. Одна проекція будь-якого елемента, розташованого в проецірующій площині, збігається з відповідним слідом цієї площини;

2. На епюрі кут нахилу заданої площини до площини проекцій проектується справжню величину (рис. 18).

3.4. Площини рівня

Особливістю площин рівня і те, будь-яка плоска постать, розташована у такій площині, проектується на паралельну їй площину без спотворення, тобто. у справжню величину (рис. 19).

Для побудови елементів, що у площині загального становища, потрібно керуватися двома правилами:

Пряма лінія належить площині, якщо вона проходить через дві точки, що лежать у площині або якщо вона проходить через точку, що лежить у площині та паралельно до іншої прямої, розташованої в цій площині (рис. 20);

Крапка лежить у площині, якщо вона лежить на прямій, розташованій у цій площині (рис. 21).

3.6. Головні лінії поверхні.

Горизонталь (h) - пряма лежача в площині і одночасно розташована паралельно площині П 1 (Рис 22). Фронталь ( f) - пряма що лежить у площині та паралельна площині П 2 . Лінія найбільшого нахилу - це пряма площина, що лежить в площині і перпендикулярна або горизонталям або фронталям площині. За допомогою лінії найбільшого нахилу визначається кут нахилу площини до площин проекцій. Лінія найбільшого нахилу розташована перпендикулярно до горизонталів площини називається ще лінією ската площини (ВК рис 22).

За допомогою лінії схилу визначається кут нахилу площини АВСдо горизонтальної поверхні проекцій. Для цього необхідно способом прямокутного трикутника визначити її натуральну величину та кут між натуральною величиною та горизонтальною проекцією буде шуканий кут.

3.7. Запитання для самоперевірки.

Перерахуйте та зобразіть графічні способи завдання площини на комплексному кресленні.

Що розуміють під слідом площини?

Яку площину називають проеціюючою та які її графічні ознаки на кресленні?

Дайте графічні характеристики площин: горизонтально - проецірующей, фронтально - проецірующей, профільно - проецірующей.

Яку площину називають площиною рівня?

Яку площину називають горизонтальною? Фронтальної? Профільний? Намалюйте їх на кресленні.

Назвіть ознаки належності прямої площини, точки площини.

Покажіть на кресленні, як можна прямо укласти в площину.

Назвіть основні лінії площини.

Як визначити кут нахилу площини горизонтальної площини проекцій?

Тепер ми перерахуємо основні методи завдання конкретної площині у просторі.

По-перше, площину можна задати, зафіксувавши три простори, що не лежать на одній прямій точці. Цей спосіб заснований на аксіомі: через будь-які три точки, що не лежать на одній прямій, проходить єдина площина.

Якщо у тривимірному просторі зафіксовано прямокутна системакоординат і задана площина за допомогою вказівки координат трьох її різних точок, що не лежать на одній прямій, ми можемо написати рівняння площини, що проходить через три задані точки.

Два наступні способи завдання площини є наслідком попереднього. Вони засновані на слідствах з аксіоми про площину через три точки:

· Через пряму та не лежачу на ній точку проходить площину, притому тільки одна (дивіться також статтю рівняння площини, що проходить через пряму та точку);

· Через дві прямі, що перетинаються, проходить єдина площина (рекомендуємо ознайомитися з матеріалом статті рівняння площини, що проходить через дві прямі, що перетинаються).

Четвертий спосіб завдання площини у просторі ґрунтується на визначенні паралельних прямих. Нагадаємо, що дві прямі у просторі називаються паралельними, якщо вони лежать в одній площині та не перетинаються. Таким чином, вказавши дві паралельні прямі у просторі, ми визначимо єдину площину, у якій ці прямі лежать.

Якщо у тривимірному просторі щодо прямокутної системи координат задана площина вказаним способом, то ми можемо скласти рівняння площини, що проходить через дві паралельні прямі.

Ознака паралельності двох площин дає нам ще один спосіб завдання площини. Згадаймо формулювання цієї ознаки: якщо дві прямі однієї площини, що перетинаються, відповідно паралельні двом прямим інший площині, то такі площини паралельні. Отже, ми можемо задати конкретну площину, якщо вкажемо точку, якою вона проходить і площину, якою вона паралельна.

У курсі середньої школи під час уроків геометрії доводиться така теорема: через фіксовану точку простору проходить єдина площина, перпендикулярна до цієї прямої. Таким чином, ми можемо задати площину, якщо вкажемо точку, якою вона проходить, і пряму, перпендикулярну до неї.

Якщо в тривимірному просторі зафіксована прямокутна система координат і задана площину вказаним способом, то можна скласти рівняння площини, що проходить через задану точку перпендикулярно заданої прямої.

Замість прямої, перпендикулярної до площини, можна вказати один із нормальних векторів цієї площини. І тут є можливість написати загальне рівнянняплощині.

Ви також можете знайти цікаву інформацію в науковому пошуковику Otvety.Online. Скористайтеся формою пошуку:

Ще за темою Способи завдання площини:

1. 13. Розлади мислення: за темпом, строєм, цілеспрямованістю. Діагностичне значення симптомів.
2. Основні напрями дослідження порушень мислення при шизофренії.
3. Класифікація порушень мислення на роботах Б.В. Зейгарник.
4. 8. Аналіз специфіки методів спеціальної психології проти методами інших галузей психології: використання стандартизованих технік (тестів), використання анкетування, методу аналізу продуктів діяльності.
5. 14. Методика вивчення площі геометричних фігур та формування навичок її виміру. Ознайомлення з одиницями виміру площі та їх співвідношенням. Особливості сприйняття молодшого школяра. Облік закономірностей та принципів виховання щодо площі геометричних фігур.

У планіметрії площина є однією з основних фігур, тому дуже важливо мати ясне уявлення про неї. Ця стаття створена для розкриття цієї теми. Спочатку дано поняття площини, її графічне уявлення та показані позначення площин. Далі площина розглядається разом із точкою, прямою чи іншою площиною, у своїй виникають варіанти із взаємного розташування просторі. У другому і третьому та четвертому пункті статті якраз розібрано всі варіанти взаємного розташування двох площин, прямої та площини, а також точки та площини, наведено основні аксіоми та графічні ілюстрації. У висновку дано основні способи завдання площини у просторі.

Навігація на сторінці.

Площина – основні поняття, позначення та зображення.

Найпростішими та основними геометричними фігурами у тривимірному просторі є точка, пряма та площина. Ми вже маємо уявлення про точку та пряму на площині. Якщо помістити площину, де зображені точки і прямі, в тривимірне простір, ми отримаємо точки і прямі у просторі. Уявлення про площину у просторі дозволяє отримати, наприклад, поверхню столу чи стіни. Однак, стіл або стіна мають кінцеві розміри, а площина тягнеться за їх межі в нескінченність.

Крапки і прямі у просторі позначаються як і площині – великими і маленькими латинськими літерами відповідно. Наприклад, точки А і Q прямі а і d . Якщо задані дві точки, що лежать на прямій, то можна позначити пряму двома літерами, що відповідають цим точкам. Наприклад, пряма АВ чи ВА проходить через точки А та В . Площини прийнято позначати дрібними грецькими літерами, наприклад, площині , або .

При вирішенні завдань виникає необхідність зображати площину на кресленні. Площина зазвичай зображують у вигляді паралелограма або довільної простої замкнутої області.

Площина зазвичай розглядається разом з точками, прямими або іншими площинами, при цьому виникають різні варіанти їхнього взаємного розташування. Переходимо до їхнього опису.

Взаємне розташування площини та точки.

Почнемо з аксіоми: у кожному площині є точки. З неї випливає перший варіант взаємного розташування площини та точки – точка може належати площині. Іншими словами, поверхня може проходити через точку. Для позначення приналежності будь-якої точки будь-якої площини використовують символ "". Наприклад, якщо площина проходить через точку А , можна коротко записати .

Слід розуміти, що на заданій площині у просторі є безліч точок.

Наступна аксіома показує, скільки точок у просторі необхідно відзначити, щоб вони визначали конкретну площину: через три точки, що не лежать на одній прямій, проходить площину, причому лише одна. Якщо відомі три точки, що лежать у площині, то площину можна позначити трьома літерами, що відповідають цим точкам. Наприклад, якщо площина проходить через точки А, В та С, то її можна позначити АВС.

Сформулюємо ще одну аксіому, яка дає другий варіант взаємного розташування площини та точки: є, принаймні, чотири точки, що не лежать в одній площині. Отже, точка простору може належати площині. Дійсно, через попередню аксіому через три точки простору проходить площина, а четверта точка може як лежати на цій площині, так і не лежати. При короткому записі використовують символ "", який рівносильний фразі "не належить".

Наприклад, якщо точка А не лежить у площині, то використовують короткий запис.

Пряма та площина у просторі.

По-перше, пряма може лежати у площині. В цьому випадку, у площині лежать хоча б дві точки цієї прямої. Це встановлюється аксіомою: якщо дві точки прямої лежать у площині, всі точки цієї прямої лежать у площині. Для короткого запису належності деякої прямої даної площини користуються символом "". Наприклад, запис означає, що пряма лежить у площині .

По-друге, пряма може перетинати площину. При цьому пряма та площина мають одну єдину загальну точку, яку називають точкою перетину прямої та площини. При короткому записі перетин позначаю символом «». Наприклад, запис означає, що пряма перетинає площину в точці М . При перетині площини деякої прямої виникає поняття кута між прямою та площиною.

Окремо варто зупинитися на прямій, яка перетинає площину та перпендикулярна будь-якій прямій, що лежить у цій площині. Таку пряму називають перпендикулярною до площини. Для короткого запису перпендикулярності використовують символ «». Для більш глибокого вивчення матеріалу можете звернутися до статті перпендикулярність прямої та площини.

p align="justify"> Особливу значимість при вирішенні завдань, пов'язаних з площиною, має так званий нормальний вектор площини. Нормальним вектором площини є будь-який ненульовий вектор, що лежить на прямій перпендикулярній цій площині.

По-третє, пряма може бути паралельна площині, тобто не мати в ній загальних точок. Під час короткого запису паралельності використовують символ «». Наприклад, якщо пряма паралельна площині , то можна записати . Рекомендуємо докладніше вивчити цей випадок, звернувшись до статті паралельність прямої та площині.

Слід сказати, що пряма, що лежить у площині, поділяє цю площину на дві півплощини. Пряма у разі називається межею полуплоскостей. Будь-які дві точки однієї півплощини лежать по одну сторону від прямої, а дві точки різних напівплощин лежать по різні боки від граничної прямої.

Взаємне розташування площин.

Дві площини у просторі можуть збігатися. У цьому випадку вони мають принаймні три загальні точки.

Дві площини у просторі можуть перетинатися. Перетином двох площин є пряма лінія, що встановлюється аксіомою: якщо дві площини мають спільну точку, вони мають спільну пряму, на якій лежать всі загальні точки цих площин.

У цьому випадку виникає поняття кута між площинами, що перетинаються. Окремий інтерес представляє випадок, коли кут між площинами дорівнює дев'яносто градусам. Такі поверхні називають перпендикулярними. Про них ми поговорили у статті перпендикулярність площин.

Нарешті, дві площини у просторі можуть бути паралельними, тобто не мати спільних точок. Рекомендуємо ознайомитися зі статтею паралельність площин, щоб отримати повне уявлення про цей варіант взаємного розташування площин.

Способи завдання площини.

Тепер ми перерахуємо основні методи завдання конкретної площині у просторі.

По-перше, площину можна задати, зафіксувавши три простори, що не лежать на одній прямій точці. Цей спосіб заснований на аксіомі: через будь-які три точки, що не лежать на одній прямій, проходить єдина площина.

Якщо в тривимірному просторі зафіксована і задана площина за допомогою вказівки координат трьох різних точок, що не лежать на одній прямій, то ми можемо написати рівняння площини, що проходить через три задані точки .

Два наступні способи завдання площини є наслідком попереднього. Вони засновані на слідствах з аксіоми про площину через три точки:

• через пряму і не лежачу на ній точку проходить площину, притому лише одна (дивіться також статтю рівняння площини, що проходить через пряму та точку);
• через дві прямі, що перетинаються, проходить єдина площина (рекомендуємо ознайомитися з матеріалом статті рівняння площини, що проходить через дві прямі, що перетинаються).

Четвертий спосіб завдання площини у просторі заснований на визначенні паралельних прямих. Нагадаємо, що дві прямі у просторі називаються паралельними, якщо вони лежать в одній площині та не перетинаються. Таким чином, вказавши дві паралельні прямі у просторі, ми визначимо єдину площину, у якій ці прямі лежать.

Якщо тривимірному просторі щодо прямокутної системи координат задана площину зазначеним способом, ми можемо скласти рівняння площині, що проходить через дві паралельні прямі .

У курсі середньої школи під час уроків геометрії доводиться така теорема: через фіксовану точку простору проходить єдина площина, перпендикулярна до цієї прямої. Таким чином, ми можемо задати площину, якщо вкажемо точку, якою вона проходить, і пряму, перпендикулярну до неї.

Якщо в тривимірному просторі зафіксована прямокутна система координат і задана площину вказаним способом, то можна скласти рівняння площини, що проходить через задану точку перпендикулярно заданої прямої.

Замість прямої, перпендикулярної до площини, можна вказати один із нормальних векторів цієї площини. І тут є можливість написати

Положення площини у просторі визначається:

• трьома точками, що не лежать на одній прямій;
• прямою та точкою, взятою поза прямою;
• двома прямими, що перетинаються;
• двома паралельними прямими;
• плоских фігур.

Відповідно до цього на епюрі площина може бути задана:

• проекціями трьох точок, що не лежать на одній прямій (Малюнок 3.1,а);
• проекціями точки та прямої (Малюнок 3.1,б);
• проекціями двох прямих, що перетинаються (Малюнок 3.1,в);
• проекціями двох паралельних прямих (Малюнок 3.1, г);
• плоскою фігурою (Малюнок 3.1, д);
• слідами площини;
• лінією найбільшого схилу площини.

Рисунок 3.1 – Способи завдання площин

Площина загального стану– це площина, яка паралельна і перпендикулярна жодної з площин проекцій.

За площиноюназивається пряма, отримана внаслідок перетину заданої площини з однією з площин проекцій.

Площина загального становища може мати три сліди: горизонтальний – απ 1 , фронтальний – απ 2 та профільний – απ 3 , які вона утворює при перетині з відомими площинами проекцій: горизонтальною π 1 фронтальної π 2 і профільної π 3 (Малюнок 3.2).

Рисунок 3.2 – Сліди площини загального стану

3.2. Площини приватного стану

Площина приватного стану- Площина, перпендикулярна або паралельна площині проекцій.

Площина, перпендикулярна площині проекцій, називається проецірующей і на цю площину проекцій вона проектуватиметься у вигляді прямої лінії.

Властивість проекції площини: усі точки, лінії, плоскі фігури, що належать проєціруючої площині, мають проекції на похилому сліді площини(Малюнок 3.3).

Рисунок 3.3 – Фронтально-проєціруюча площина, якій належать: точки А, В, З; лінії АС, АВ, НД; площину трикутника АВС

Фронтально-проекційна площина – площина, перпендикулярна фронтальній площині проекцій(Малюнок 3.4, а).

Горизонтально-проецуюча площина – площина перпендикулярна горизонтальній площині проекцій(Малюнок 3.4, б).

Профільно-проецуюча площина – площина, перпендикулярна профільній площині проекцій.

Площини, паралельні площинам проекцій, називаються площинами рівняабо двічі проецірующими площинами.

Фронтальна площина рівня – площина, паралельна фронтальній площині проекцій(Малюнок 3.4, в).

Горизонтальна площина рівня – площина, паралельна горизонтальній площині проекцій(Малюнок 3.4, г).

Профільна площина рівня – площина, паралельна профільній площині проекцій(Малюнок 3.4, д).

Рисунок 3.4 – Епюри площин приватного стану

3.3. Крапка і пряма в площині. Приналежність точки та прямої площини

Крапка належить площині, якщо вона належить будь-якій прямій, що лежить у цій площині(Малюнок 3.5).

Пряма належить площині, якщо вона має із площиною хоча б дві загальні точки(Малюнок 3.6).

Рисунок 3.5 – Приналежність точки площини

α = m // n

D∈ n⇒ D∈ α

Рисунок 3.6 – Приналежність до прямої площини

Вправа

Дано площину, задану чотирикутником (Малюнок 3.7, а). Необхідно добудувати горизонтальну проекцію вершини З.

а	б

Рисунок 3.7 – Розв'язання задачі

Рішення :

1. ABCD- Плоский чотирикутник, що задає площину.
2. Проведемо у ньому діагоналі ACі BD(Малюнок 3.7, б), які є прямими, що перетинаються, також задають ту ж площину.
3. Згідно з ознакою прямих, що перетинаються, побудуємо горизонтальну проекцію точки перетину цих прямих. Kз її відомої фронтальної проекції: A 2 C 2 ∩ B 2 D 2 =K 2 .
4. Відновимо лінію проекційного зв'язку до перетину з горизонтальною проекцією прямої BD: на проекції діагоналі B 1 D 1 будуємо До 1 .
5. Через А 1 До 1 проводимо проекцію діагоналі А 1 З 1 .
6. Крапку З 1 отримуємо, за допомогою лінії проекційного зв'язку до перетину її з горизонтальною проекцією продовженої діагоналі А 1 До 1 .

3.4. Головні лінії площини

У площині можна побудувати безліч прямих, але є особливі прямі, що лежать у площині, звані головними лініями площини (Малюнок 3.8 – 3.11).

Прямий рівень або паралеллю площининазивається пряма, що лежить у даній площині і паралельна до однієї з площин проекцій.

Горизонталь або горизонтальна пряма рівня h(перша паралель) – це пряма, що лежить у даній площині та паралельна горизонтальній площині проекцій (π 1)(Малюнок 3.8, а; 3.9).

Фронталь або фронтальна пряма рівня f(друга паралель) – це пряма лежача в даній площині та паралельна фронтальній площині проекцій (π 2)(Малюнок 3.8, б; 3.10).

Профільна пряма рівня p(третя паралель) – це пряма площина, що лежить в даній площині, і паралельна профільній площині проекцій (π 3)(Малюнок 3.8, ст; 3.11).

Рисунок 3.8 а – Горизонтальна пряма рівня у площині, заданій трикутником

Рисунок 3.8 б – Фронтальна пряма рівня у площині, заданій трикутником

Рисунок 3.8 в – Профільна пряма рівня площині, заданої трикутником

Рисунок 3.9 – Горизонтальна пряма рівня площині, заданої слідами

Рисунок 3.10 – Фронтальна пряма рівня площині, заданої слідами

Рисунок 3.11 – Профільна пряма рівня у площині, заданій слідами

3.5. Взаємне положення прямої та площини

Пряма по відношенню до заданої площини може бути паралельною і може мати загальну точку, тобто перетинатися.

3.5.1. Паралельність прямої площини

Ознака паралельності прямої площини: пряма паралельна площині, якщо вона паралельна будь-якій прямій, що належить цій площині(Малюнок 3.12).

Рисунок 3.12 – Паралельність прямої площини

3.5.2. Перетин прямої з площиною

Для побудови точки перетину прямої з площиною загального положення (Малюнок 3.13) необхідно:

1. Укласти пряму ау допоміжну площину β (як допоміжна площина слід вибирати площини приватного положення);
2. Знайти лінію перетину допоміжної площини β із заданою площиною α;
3. Знайти точку перетину заданої прямої аз лінією перетину площин MN.

Рисунок 3.13 – Побудова точки зустрічі прямої із площиною

Вправа

Задані: пряма АВзагального стану, площина σ⊥π 1 . (Малюнок 3.14). Побудувати точку перетину прямої АВіз площиною σ.

Рішення :

1. Площина σ – горизонтально-проецуюча, отже, горизонтальною проекцією площини є пряма σ 1 (горизонтальний слід площини);
2. Точка, крапка Домає належати прямий АВ ⇒ До 1 ∈А 1 В 1 та заданої площини σ ⇒ До 1 ∈σ 1 , отже, До 1 знаходиться в точці перетину проекцій А 1 В 1 і σ 1;
3. Фронтальну проекцію точки Дознаходимо за допомогою лінії проекційного зв'язку: До 2 ∈А 2 В 2 .

Рисунок 3.14 – Перетин прямого загального стану з площиною приватного положення

Вправа

Задано: площину σ = Δ АВС– загального стану, пряма EF(Малюнок 3.15).

Потрібно побудувати точку перетину прямої EFіз площиною σ.

а	б

Рисунок 3.15 – Перетин прямої з площиною

1. Заключимо пряму EFу допоміжну площину, якою скористаємося горизонтально-проецірующей площиною α (Малюнок 3.15, а);
2. Якщо α⊥π 1 , то на площину проекцій π 1 площина α проектується в пряму (горизонтальний слід площини απ 1 або α 1), що збігається з E 1 F 1 ;
3. Знайдемо пряму перетину (1-2) проецірующей площині α з площиною σ (вирішення подібного завдання буде розглянуто);
4. Пряма (1-2) та задана пряма EFлежать в одній площині і перетинаються в точці K.

Алгоритм розв'язання задачі (Малюнок 3.15, б):

Через EFпроведемо допоміжну площину α:

3.6. Визначення видимості методом конкуруючих точок

Оцінюючи положення цієї прямої, необхідно визначити – точка якої ділянки прямої розташована ближче (далі) до нас, як до спостерігачів, при погляді на площину проекцій π 1 або π 2 .

Точки, які належать різним об'єктам, але в одній із площин проекцій їх проекції збігаються (тобто, дві точки проектуються на одну), називаються конкуруючими у цій площині проекцій.

Необхідно окремо визначити видимість кожної площині проекцій.

Видимість на π 2 (рис. 3.15)

Виберемо точки, що конкурують на π 2 – точки 3 та 4. Нехай точка 3∈ ВС∈σ, точка 4∈ EF.

Щоб визначити видимість точок на площині проекцій π 2, треба визначити розташування цих точок на горизонтальній площині проекцій при погляді на π 2 .

Напрямок погляду на π 2 показано стрілкою.

По горизонтальних проекціях точок 3 і 4, при погляді на π 2 видно, що точка 4 1 розташовується ближче до спостерігача, ніж 3 1 .

4 1 ∈E 1 F 1 ⇒ 4∈EF⇒ на π 2 буде видно точку 4, що лежить на прямій EF, отже, пряма EFна ділянці розглянутих конкуруючих точок розташована перед площиною σ і буде видно до точки K

Видимість на π 1

Для визначення видимості оберемо точки, які конкурують на π 1 – точки 2 та 5.

Щоб визначити видимість точок на площині проекцій 1 потрібно визначити розташування цих точок на фронтальній площині проекцій при погляді на 1 .

Напрямок погляду на π 1 показано стрілкою.

По фронтальним проекціям точок 2 і 5, при погляді на π 1 видно, що точка 2 2 розташовується ближче до спостерігача, ніж 5 2 .

2 1 ∈А 2 В 2 ⇒ 2∈АВ⇒ на π 1 буде видно точку 2, що лежить на прямій АВ, отже, пряма EFна ділянці розглянутих конкуруючих точок розташована під площиною σ і буде невидима до точки K– точки перетину прямої із площиною σ.

Очевидною з двох конкуруючих точок буде та, у якої координата «Z» або (і) «Y» більша.

3.7. Перпендикулярність прямої площини

Ознака перпендикулярності прямої площини: пряма перпендикулярна площині, якщо вона перпендикулярна двом прямим, що перетинаються, лежать у даній площині.

а	б

Рисунок 3.16 – Завдання прямої, перпендикулярної площині

Теорема. Якщо пряма перпендикулярна площині, то на епюрі: горизонтальна проекція прямої перпендикулярна горизонтальній проекції горизонталі площини, а фронтальна проекція прямої перпендикулярна фронтальній проекції фронталі (Малюнок 3.16, б)

Теорема доводиться через теорему про проектування прямого кута в окремому випадку.

Якщо площина задана слідами, то проекції прямої перпендикулярної площини перпендикулярні до відповідних слідів площини (Малюнок 3.16, а).

Нехай пряма pперпендикулярна до площини σ=Δ АВСі проходить через точку K.

1. Побудуємо горизонталь та фронталь у площині σ=Δ АВС : A-1∈σ; A-1//π 1; С-2∈σ; С-2//π 2 .
2. Відновимо з точки Kперпендикуляр до заданої площини: p 1⊥h 1і p 2⊥f 2, або p 1⊥απ 1 і p 2⊥απ 2

3.8. Взаємне становище двох площин

3.8.1. Паралельність площин

Дві площини можуть бути паралельними і такими, що перетинаються між собою.

Ознака паралельності двох площин: дві площини взаємно паралельні, якщо дві прямі однієї площини, що перетинаються, відповідно паралельні двом перетинаються прямим інший площині.

Вправа

Задано площину загального стану α=Δ АВСі крапка F∉α (Малюнок 3.17).

Через точку Fпровести площину β, паралельну площині α.

Рисунок 3.17 – Побудова площини паралельної заданої

Рішення :

Як прямі площини α, що перетинаються, візьмемо, наприклад, сторони трикутника АВ і ВС.

1. Через точку Fпроводимо пряму m, паралельну, наприклад, АВ.
2. Через точку F, або через будь-яку точку, що належить m, проводимо пряму n, паралельну, наприклад, НД, причому m∩n=F.
3. β = m∩nта β//α за визначенням.

3.8.2. Перетин площин

Результатом перетину 2-х площин є пряма. Будь-яка пряма на площині або просторі може бути однозначно задана двома точками. Тому для того, щоб побудувати лінію перетину двох площин, слід знайти дві точки, спільні для обох площин, після чого з'єднати їх.

Розглянемо приклади перетину двох площин при різних способах їх завдання: слідами; трьома точками, що не лежать на одній прямій; паралельними прямими; прямими, що перетинаються, та ін.

Вправа

Дві площини α та β задані слідами (Малюнок 3.18). Побудувати лінію перетину площин.

Рисунок 3.18 – Перетин площин загального стану, заданих слідами

Порядок побудови лінії перетину площин:

1. Знайти точку перетину горизонтальних слідів - це точка М(її проекції М 1 і М 2 , при цьому М 1 =М, т.к. М -точка приватного стану, що належить площині π 1).
2. Знайти точку перетину фронтальних слідів – це точка N(її проекції N 1 та N 2 , при цьому N 2 = N, т.к. N -точка приватного стану, що належить площині π 2).
3. Побудувати лінію перетину площин, з'єднавши однойменні проекції отриманих точок: М 1 N 1 та М 2 N 2 .

МN- Лінія перетину площин.

Вправа

Задано площину σ = Δ АВС, площина α – горизонтально-проеціююча (α⊥π 1) ⇒α 1 – горизонтальний слід площини (Малюнок 3.19).

Побудувати лінію перетину цих площин.

Рішення :

Оскільки площина α перетинає сторони АВі АСтрикутника АВСто точки перетину Kі Lцих сторін з площиною є спільними для обох заданих площин, що дозволить, з'єднавши їх, знайти лінію перетину.

Точки можуть бути знайдені як точки перетину прямих з проеціюючою площиною: знаходимо горизонтальні проекції точок Kі L, тобто K 1 та L 1 на перетині горизонтального сліду (α 1) заданої площини α з горизонтальними проекціями сторін Δ АВС: А 1 В 1 та A 1 C 1 . Після цього за допомогою ліній проекційного зв'язку знаходимо фронтальні проекції цих точок K 2і L 2 на фронтальних проекціях прямих АВі АС. Поєднаємо однойменні проекції: K 1 та L 1 ; K 2і L 2 . Лінія перетину заданих площин побудована.

Алгоритм розв'язання задачі:

KL- Лінія перетину Δ АВСі σ (α∩σ = KL).

Рисунок 3.19 – Перетин площин загального та приватного стану

Вправа

Задано площини α = m//n та площину β = Δ АВС(Малюнок 3.20).

Побудувати лінію перетину заданих площин.

Рішення :

1. Щоб знайти точки, спільні для обох заданих площин і задають лінію перетину площин α і β, необхідно скористатися допоміжними площинами приватного положення.
2. Як такі площини виберемо дві допоміжні площини приватного стану, наприклад: σ // τ; σ⊥π 2; τ⊥π 2 .
3. Знову введені площини перетинаються з кожною із заданих площин α і β за прямими, паралельними один одному, оскільки σ // τ:

- результатом перетину площин α, σ і τ є прямі (4-5) та (6-7);

- результатом перетину площин β, σ і τ є прямі (3-2) та (1-8).

1. Прямі (4-5) та (3-2) лежать у площині σ; точка їх перетину Модночасно лежить у площинах і β, тобто на прямій перетину цих площин;
2. Аналогічно знаходимо точку N, загальну для площин α та β.
3. З'єднавши точки Mі N, побудуємо пряму перетин площин α і β.

Рисунок 3.20 – Перетин двох площин загального стану (загальний випадок)

Алгоритм розв'язання задачі:

Вправа

Задані площини α = Δ АВСта β = a//b. Побудувати лінію перетину заданих площин (Малюнок 3.21).

Рисунок 3.21 Розв'язання задачі на перетин площин

Рішення :

Скористаємося допоміжними площинами приватного положення. Введемо їх так, щоб скоротити кількість побудов. Наприклад, введемо площину σ⊥π 2 , уклавши пряму aу допоміжну площину σ (σ∈ a). Площина σ перетинає площину α по прямій (1-2), а σ∩β= а. Отже (1-2)∩ а=K.

Точка, крапка Доналежить обом площинам α та β.

Отже, точка K, є однією з точок, через які проходить пряма перетину заданих площин α і β.

Для знаходження другої точки, що належить прямій перетину α і β, заключимо пряму bу допоміжну площину τ⊥π 2 (τ∈ b).

З'єднавши точки Kі L, Отримаємо пряму перетину площин α і β.

3.8.3. Взаємно перпендикулярні площині

Площини взаємно перпендикулярні, якщо одна з них проходить через перпендикуляр до іншої.

Вправа

Задано площину σ⊥π 2 та пряма загального становища – DE(Малюнок 3.22)

Потрібно побудувати через DEплощину τ⊥σ.

Рішення .

Проведемо перпендикуляр CDдо площини σ – C 2 D 2 ⊥σ 2 (на підставі).

Малюнок 3.22 – Побудова площини, перпендикулярної до заданої площини

За теоремою про проектування прямого кута C 1 D 1 має бути паралельна осі проекцій. Пересічні прямі CD∩DEзадають площину? Отже, τ⊥σ.

Аналогічні міркування, у разі площини загального становища.

Вправа

Задано площину α = Δ АВСі крапка Kпоза площиною α.

Потрібно побудувати площину β⊥α, що проходить через точку K.

Алгоритм рішення(Малюнок 3.23):

1. Побудуємо горизонталь hта фронталь fу заданій площині α = Δ АВС;
2. Через точку Kпроведемо перпендикуляр bдо площини α (по теоремі про перпендикуляр до площини: якщо пряма перпендикулярна до площини, то її проекції перпендикулярні до похилих проекцій горизонталі та фронталі, що лежать у площині:b 2⊥f 2; b 1⊥h 1;
3. Задаємо площину β будь-яким способом, наприклад, β = a∩b, таким чином, площина перпендикулярна до заданої побудована: α⊥β.

Рисунок 3.23 – Побудова площини перпендикулярної до заданої Δ АВС

3.9. Завдання для самостійного вирішення

1. Задано площину α = m//n(Малюнок 3.24). Відомо що K∈α.

Побудуйте передню проекцію точки До.

Малюнок 3.24

2. Побудуйте сліди прямою, заданою відрізком CB, та визначте квадранти, через які вона проходить (Малюнок 3.25).

Малюнок 3.25

3. Побудуйте проекції квадрата, що належить площині α⊥π 2 якщо його діагональ MN//π 2 (Малюнок 3.26).

Малюнок 3.26

4. Побудувати прямокутник ABCDз більшою стороною НДна прямий m, Виходячи з умови, що відношення його сторін дорівнює 2 (Малюнок 3.27).

Малюнок 3.27

5. Задано площину α= a//b(Малюнок 3.28). Побудувати площину β паралельну площині α та віддалену від неї на відстані 20 мм.

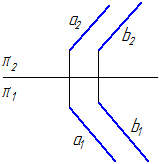
Малюнок 3.28

6. Задано площину α=∆ АВСі крапка D Dплощину β⊥α та β⊥π 1 .

7. Задано площину α=∆ АВСі крапка Dпоза площиною. Побудувати через точку Dпряму DE//α та DE//π 1 .